How to Find Order-up-to Level in a Periodic Review System

Appendix A. Derivations leading to the procedure for selecting values of southward and S

A.one. E(τ) and Var(τ) for a given value of S−s

Equally indicated in Figure A.i (which reflects setting R=1), τ is the fourth dimension from the instant that the inventory position first reaches s until the moment of the next review. The behaviour of cumulative normally distributed demand (hence the modify in the inventory position away from the order-upwards-to-level, S) tin can exist modelled every bit a continuous time diffusion process (Miltenburg and Silver, 1984). Moreover, the probability density function of the first passage time, u, for the inventory position to drop from S to s is given by (Cox and Miller, 1965)

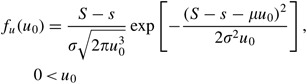
Setting

and

we obtain

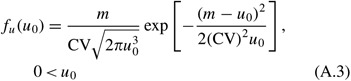
Equally an bated, Burgin (1969) developed an analytic expression for the expected value of u.

Figure A.one

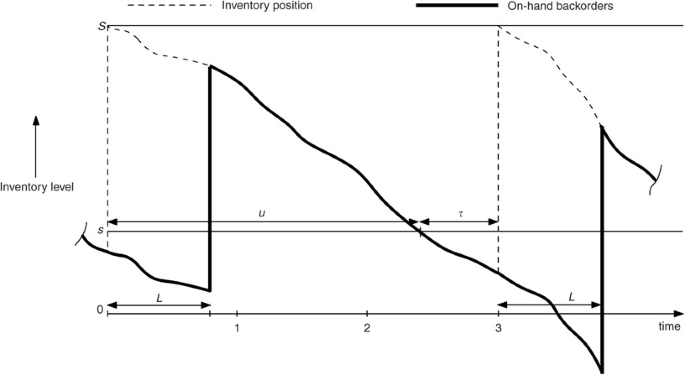
Relation between first passage time (u) and τ.

Total size paradigm

Now, multiple values of u can produce the same value of τ. Specifically τ=τ ₀ will issue from whatsoever of u=1−τ ₀, 2−τ ₀, etc. Hence, the density function of τ is given past

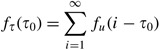
Using (A.3) nosotros have

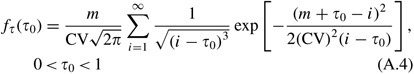
Unfortunately, it is non possible to analytically develop expressions for the moments of τ. All the same, note that the density function, hence the moments, depend on only two parameters, namely m and CV. For given values of these parameters τ ₀ tin be discretized on a fine filigree and accurate estimates of E(τ) and Var(τ) can be found by numerical integration.

A.2. Determining South−southward to target the desired average fourth dimension betwixt replenishments (besides leading to Step one of the procedure)

For a given value of τ the expected size of the undershoot

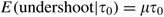
Hence E(undershoot)=μ E(τ). Allow Q denote the society size. Then, the average gild size

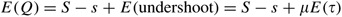
The average time betwixt replenishments

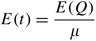
Using (A.1), E(t)=m+E(τ). But nosotros want to target an integer n for Due east(t). Thus we require

Now E(τ) is a function of both grand and CV. Thus, for a given value of CV we have to find the m that satisfies (A.5). This was done using Mathematica where for each value of m, equally mentioned earlier, numerical integration is needed to approximate East(τ). Rather than providing detailed tables of Due east(τ) versus CV, for several practical values of north we have instead used Stata (Stata Corp., 2003) to fit fractional polynomial functions of caste iii (with very loftier R ² values). The results of fitting functions to 51 values of East(τ), resulting from equi-spaced values of CV between 0.1 and 0.5, are shown in Tabular array i. Note that the powers of CV accept been adjusted to the average CV value (0.3) in the approximation expressions; come across the Stata Base Reference Manual (Vol. 1, pp 402–403) for farther information.

In the higher up, once the m is establish that satisfies (A.five) for given values of n and CV, we then use numerical integration to estimate Var(τ). Over again, very accurate fractional polynomial functions were fit to Var(τ) as a role of CV for selected values of northward, as shown in Table 2.

A.3. Determining due south to give a desired service level (Steps 2, 3 and 4 of the process)

As discussed in the previous subsection, for given values of due north and CV we are able to determine E(τ) and Var(τ). Allow X represent the total demand in the constructive atomic number 82 fourth dimension τ+L. As evident in Figure 1, a shortage volition occur if X exceeds the reorder point south. We can model the situation as a continuous review, reorder point system where the effective lead fourth dimension τ+L is a random variable with hateful East(τ)+L and variance Var(τ). Nether such circumstances X has moments (see Silverish et al, 1998, p 283)

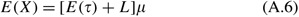
and

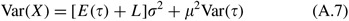
Dividing (A.6) by μ and (A.7) past μ ^two we take

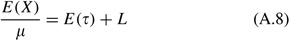
and

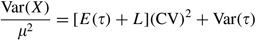
Taking the square root of the latter results in

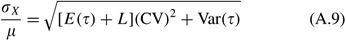
In the usual fashion, set south=E(10)+k σ ₁₀ . It is again convenient to carve up through by μ to obtain

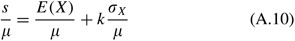
If we assume that X is normally distributed (which we know is an approximation considering τ is a random variable; withal, Tyworth and O'Neill (1997) and Silvery et al (1998, pp 272–273) fence that equally long equally σ _X /E(X)⩽0.5, there is piffling risk in making the normality assumption), and then use of (A.2) leads to the expected units short per replenishment bike (run across Silvery et al, 1998)

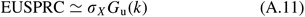
where

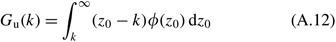
is the unit normal loss function and φ(z ₀) is the unit normal density function. Note that at that place is a more precise version of (A.12) which turned out to not be required in our numerical experiments, specifically

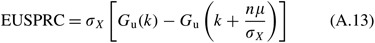
The target immune (average) units brusque per replenishment cycle

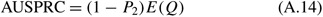
From (A.xi) and (A.14) and noting that Eastward(Q)=n μ, we thus require

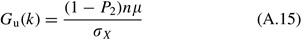
A.4. Determining the Southward value (Stride 5)

Utilize of (A.1) and (A.5) gives

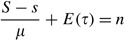
Hence

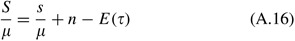
Appendix B. Some technical details of the simulation

To estimate the fill up rate achieved, we accept used the 'virtual measures' arroyo of variance reduction first suggested by Carter and Ignall (1975). Specifically, permit I _i (⩽s) be the inventory position when the ith order (of size Q _i ) is placed. Then (for reference purposes run across (A.xiii)) the expected units curt at the finish of the atomic number 82 time conditional on I _i tin can be computed analytically as

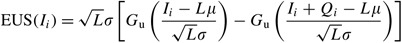
Over a large number (N) of replenishments the estimated average number of units curt per replenishment is

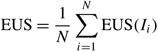
Also, I _i +Q _i =South. Thus

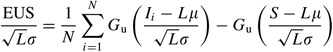
where the last term on the right-hand side is a abiding. Consequently, we merely have to compute 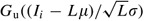for each replenishment i.

Now an estimate of the average lodge size is given by

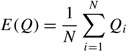
and the expected fill up rate is

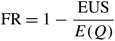
The other performance measure we demand is the average time betwixt replenishments

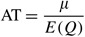
Besides point estimates of each of FR and AT, confidence intervals were developed based upon the replication–deletion method for estimating a steady-country mean (come across, eg, Law and Kelton, 2000).

wennerhickis1967.blogspot.com

Source: https://link.springer.com/article/10.1057/palgrave.jors.2602655

Share this post